22. Riemann Sums, Integrals and the FTC

d. Integration Rules and Properties

3. Definite Integral Properties

The tables on the four previous pages listed the properties of indefinite integrals. On this page, we discuss additional properties of definite integrals. All the proofs are bases on the Riemann sum definition.

Inequalities:

If the functions \(f\) and \(g\) are related by \(f \le g\) everywhere on the interval of integration, then their integrals are similarly related:

If \(f(x) \le g(x)\) for all \(x\) in \([a,b]\), then \[ \int_a^b f(x)\,dx \le \int_a^b g(x)\,dx \]

Since \(f(x) \le g(x)\), we have \[\begin{aligned} f(x_i^*) &\le g(x_i^*) \\ \sum_{i=1}^n\,f(x_i^*)\Delta x_i &\le \sum_{i=1}^n\,g(x_i^*)\Delta x_i \\ \lim_{\begin{aligned}&\scriptstyle\quad n\to\infty \\ &\scriptstyle\text{max}\Delta x_i\to0\end{aligned}} \,\sum_{i=1}^n\,f(x_i^*)\Delta x_i &\le \lim_{\begin{aligned}&\scriptstyle\quad n\to\infty \\ &\scriptstyle\text{max}\Delta x_i\to0\end{aligned}} \,\sum_{i=1}^n\,g(x_i^*)\Delta x_i \\ \int_a^b f(x)\,dx &\le \int_a^b g(x)\,dx \end{aligned}\]

Show that the area under the curve \(f(x)=x^3+x^2+3\) is greater than the area under the curve \(g(x)=x+4\) above the interval \([1,2]\), without computing any integrals.

On the interval \([1,2]\), we have \(f'(x)=3x^2+2x > 1\) and \(g'(x)=1\). So both functions are increasing on the that interval and \(f\) increases faster than \(g\). Further, the minimum value for both functions occurs at the left endpoint, \(x=1\), where \(f(1)=g(1)=5\). Therefore, \(f \ge g\) on the entire interval. This is confirmed in the plot. Therefore: \[ \int_1^2 f(x)\,dx \ge \int_1^2 g(x)\,dx \] which is the obvious statement that the area under \(f\) is greater than the area under \(g\) on the interval \([1,2]\).

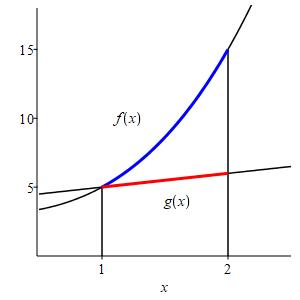
If you considered a range such as \(0 \lt x \lt 2\), you can see that \(g(x)\) is sometimes greater than \(f(x)\); therefore we would not be able to conclude anything about the relative areas. However, on the range \(1 \lt x \lt 2\), \(f(x)\) is greater than \(g(x)\); so we can conclude the area below \(f(x)\) is greater than that below \(g(x)\).

Bounds on the Integral:

In particular, if \(m\) is a lower bound for \(f\) and \(M\) is an upper bound for \(f\), then \(m \le f(x) \le M\) which leads to bounds on the integral of \(f\):

If \(m \le f(x) \le M\) then \[ m(b-a) = \int_a^b m\,dx \le \int_a^b f(x)\,dx \le \int_a^b M\,dx =M(b-a) \]

Since \(m \le f(x) \le M\), the Inequality Rule says: \[ \int_a^b m\,dx \le \int_a^b f(x)\,dx \le \int_a^b M\,dx \] Now the antiderivative of \(m\) is \(mx\) and that of \(M\) is \(Mx\). So: \[ \int_a^b m\,dx=\left[\rule{0pt}{10pt}mx\right]_a^b=m(b-a) \] and \[ \int_a^b M\,dx=\left[\rule{0pt}{10pt}Mx\right]_a^b=M(b-a) \]

Find lower and upper bounds for the integral \(\displaystyle \int_1^4 \sin^2 x\,dx\).

Since \(0 \le \sin^2 x \le 1\) for all \(x\), we conclude \[ 0=0(4-1) \le \int_1^4 \sin^2 x\,dx \le 1(4-1)=3 \]

Find lower and upper bounds for the integral \(\displaystyle \int_1^3 x^4\,dx\).

\(\displaystyle 2 \le \int_1^3 x^4\,dx \le 162\)

Since \(1 \le x^4 \le 81\) on the interval \(1 \le x \le 3\), we can conclude that the lower bound on the integral is \(L=1(3-1)=2\) and the upper bound is \(U=81(3-1)=162\): \[ 2 \le \int_1^3 x^4\,dx \le 162 \] These are not very good bounds!

Splitting the Interval

If \(a \le b \le c\), then an integral from \(a\) to \(c\), can be split at \(b\): \[ \int_a^c f(x)\,dx=\int_a^b f(x)\,dx+\int_b^c f(x)\,dx \] (This is the one proof which requires Riemann Sums with unequal intervals.)
(This one is easy.)

We start with the Riemann sum definitions of \[ \int_a^b f\,dx \quad \text{and} \quad \int_b^c f\,dx \] Partition \([a,b]\) into \(n_1\) subregions \([x_{i-1},x_i]\) of width \(\Delta x_i=x_i-x_{i-1}\) for \(i=1,2,\ldots,n_1\).
Partition \([b,c]\) into \(n_2\) subregions \([x_{j-1},x_j]\) of width \(\Delta x_j=x_j-x_{j-1}\) for \(j=n_1+1,n_1+2,\ldots,n_1+n_2\).
Note: \(n_0=a\), \(n_1=b\) and \(n_1+n_2=c\).
Then the subregions \([x_{i-1},x_i]\) and \([x_{j-1},x_j]\) are a partition of \([a,c]\) and any sum over \(i=1,\ldots,n=n_1+n_2\) is the sum over \(i=1,2,\ldots,n_1\) plus the sum over \(j=n_1+1,n_1+2,\ldots,n_1+n_2\). Further, the limit as \(n\to\infty\) can be achieved by simultaneously taking the limits as \(n_1\to\infty\) and \(n_2\to\infty\). Then: \[\begin{aligned} \int_a^c f\,dx &=\lim_{\begin{aligned}&\scriptstyle\quad n\to\infty \\ &\scriptstyle\text{max}\Delta x_i\to0\end{aligned}} \sum_{i=1}^n\,f(x_i^*)\Delta x_i \\ &=\lim_{\begin{aligned}&\scriptstyle\quad n\to\infty \\ &\scriptstyle\text{max}\Delta x_i\to0\end{aligned}} \sum_{i=1}^{n_1}\,f(x_i^*)\Delta x_i +\lim_{\begin{aligned}&\scriptstyle\quad n\to\infty \\ &\scriptstyle\text{max}\Delta x_i\to0\end{aligned}} \sum_{j=n_1+1}^{n_1+n_2}\,f(x_j^*)\Delta x_j \\ &=\int_a^b f\,dx+\int_b^c f\,dx \end{aligned}\]

Let \(F(x)\) be any antiderivative of \(f\). Then: \[\begin{aligned} \int_a^b f(x)\,dx&=F(b)-F(a) \\ \int_b^c f(x)\,dx&=F(c)-F(b) \\ \end{aligned}\] Consequently: \[\begin{aligned} \int_a^b f(x)\,dx+\int_b^c f(x)\,dx &=F(b)-F(a)+F(c)-F(b) \\ &=F(c)-F(a) =\int_a^c f(x)\,dx \end{aligned}\]

Find the area above the \(x\)-axis below both of the functions \(y=-x^2+4\) and \(y=x^2+2\) as shown in the plot.

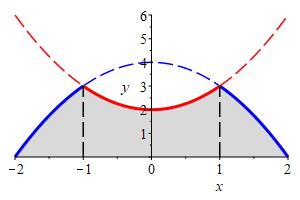
We first have to find the intersection points where we need to split the integral: \[\begin{aligned} y=-x^2+4=x^2+2 \quad &\implies \quad 2x^2=2 \\ \implies \quad x^2=1 \quad &\implies \quad x=\pm 1 \end{aligned}\] So we break up the integral at \(x=-1\) and \(x=1\) as follows: \[\begin{aligned} \int_{-2}^2 f(x)\,dx &=\int_{-2}^{-1} -x^2+4\,dx+\int_{-1}^1 x^2+2\,dx+\int_1^2 -x^2+4\,dx \\ &=\left[-\,\dfrac{x^3}{3}+4x\right]_{-2}^{-1} +\left[\dfrac{x^3}{3}+2x\right]_{-1}^1 +\left[-\,\dfrac{x^3}{3}+4x\right]_1^2 \\ &=\left[\dfrac{1}{3}-4-\dfrac{8}{3}+8\right] +\left[\dfrac{1}{3}+2+\dfrac{1}{3}+2\right] +\left[-\,\dfrac{8}{3}+8+\,\dfrac{1}{3}-4\right] \\ &=\dfrac{-12}{3}+4+4+4=8 \end{aligned}\]

Compute \(\displaystyle \int_{-1}^3 2+|x-2|\,dx\).

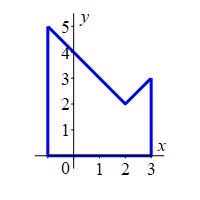
\(\displaystyle \int_{-1}^3 2+|x-2|\,dx=13\)

We split the integral at \(x=2\): \[\begin{aligned} \int_{-1}^3 2+|x-2|\,dx &=\int_{-1}^2 2+(2-x)\,dx+\int_2^3 2+(x-2))\,dx \\ &=\left[4x-\dfrac{x^2}{2}\right]_{-1}^2+\left[\dfrac{x^2}{2}\right]_2^3 \\ &=(8-2)-\left(-4-\dfrac{1}{2}\right)+\left(\dfrac{9}{2}\right)-(2) =13 \end{aligned}\] Notice that in the first step, we used: \(|x-2|=\left\{\begin{matrix} (x-2)\qquad\quad\;\; &\text{if} &x \ge 2 \\ -(x-2)=(2-x) &\text{if} &x \le 2 \end{matrix}\right.\)

We can check the answer by simply calculating the area in the plot: a \(4\times 2\) rectangle at the bottom, a \(3\times3\) right triangle at the left and a \(1\times1\) right triangle at the right. \[ 8+\dfrac{9}{2}+\dfrac{1}{2}=13 \]

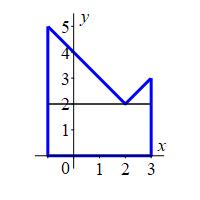
Interchanging Limits

For any numbers \(a\) and \(b\): \[ \int_b^a f(x)\,dx=-\int_a^b f(x)\,dx \] (Another easy proof.)

Let \(F(x)\) be any antiderivative of \(f\). Then: \[\begin{aligned} \int_a^b f(x)\,dx&=F(b)-F(a) \\ \int_b^a f(x)\,dx&=F(a)-F(b) \\ \end{aligned}\] Consequently: \[ \int_b^a f(x)\,dx=-\int_a^b f(x)\,dx \]

Given that \(\displaystyle \int_2^3 f(x)\,dx=7\) and \(\displaystyle \int_2^9 f(x)\,dx=5\), find \(\displaystyle \int_9^3 f(x)\,dx\).

\(\displaystyle \int_9^3 f(x)\,dx=2\)

We first split the integral \(\displaystyle \int_2^9 f(x)\,dx=5\): \[ \int_2^9 f(x)\,dx=\int_2^3 f(x)\,dx+\int_3^9 f(x)\,dx \] Consequently: \[ \int_3^9 f(x)\,dx=\int_2^9 f(x)\,dx-\int_2^3 f(x)\,dx=5-7=-2 \] Then we reverse the limits on \(\displaystyle \int_3^9 f(x)\,dx\): \[ \int_9^3 f(x)\,dx=-\int_3^9 f(x)\,dx=2 \]